How to Understand Hollow Conjugate in Simple Terms?
Understanding complex concepts often feels daunting. One such concept is "Hollow Conjugate." Renowned expert Dr. Lisa Renfield states, “Hollow Conjugate shapes our understanding of material forces.” This highlights its significance in various fields.
Hollow Conjugate plays a crucial role in physics and engineering. It refers to a specific kind of relationship where forces act in harmony. Think of it like balancing a seesaw. One side can’t function without the other. Each element must connect perfectly.
Understanding Hollow Conjugate requires careful consideration. It can easily lead to confusion if not grasped well. Visualizing it can help—but mistakes can occur. Embracing the journey of learning, including errors, can lead to growth. Hollow Conjugate isn’t just about precision; it’s about discovering new perspectives.
What is a Hollow Conjugate? A Basic Definition
Hollow conjugate is a term that may sound complex, but it's quite simple once you break it down. At its core, a hollow conjugate refers to a concept in mathematics that deals with pairs of functions. Specifically, these functions relate to one another in a unique way, highlighting their symbiotic relationship. Imagine two shapes or graphs that fit together, yet one is slightly "hollowed out" compared to the other. This hollow area often represents key insights or values in various mathematical contexts.
Understanding this concept can be tricky. Here’s a tip: visualize the function alongside its hollow counterpart. Sketching can help solidify your understanding. Take a standard function and draw its hollow conjugate next to it. Notice how the curves relate to each other.
Another useful tip is to explore practical examples. Try to apply the concept of hollow conjugates in real-world situations, like engineering or physics. This can deepen your understanding. But remember, it’s okay if the concept doesn’t click right away. Reflecting on these functions and their relationships may lead to new insights. The journey of learning often requires patience and persistence.
The Mathematical Representation of Hollow Conjugates
Hollow conjugates are an intriguing concept in mathematics. They can be defined around the relationships between certain functions. When we dig deeper, we find that they often highlight peculiarities in the behavior of these functions.
Mathematically, hollow conjugates can be represented using a variety of equations. These equations reveal how specific transformations apply to functions. A common form involves comparing original functions with their transformations. This comparison helps us understand the structure of their relationship.
Some might find these ideas abstract. However, they do exist in real situations. For instance, in geometry, hollow conjugates can illustrate the relationship between shapes. The visual representation makes it easier to grasp. But at times, the equations can be overwhelming. It requires patience and practice to master them.
There are nuances that often trip people up, leading to confusion. Understanding these details is essential for a clearer picture.
Applications of Hollow Conjugates in Geometry and Physics
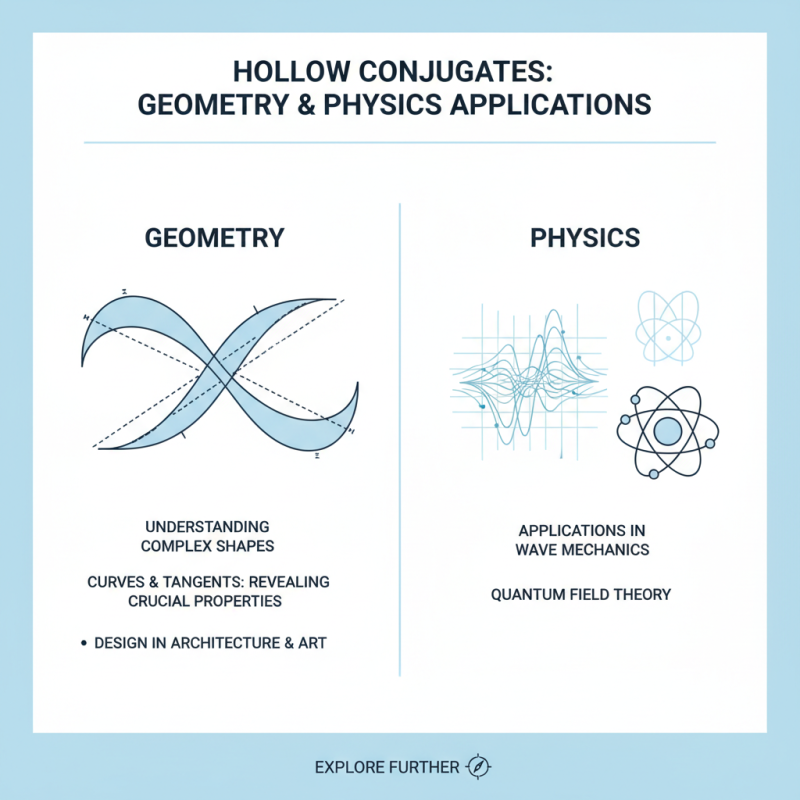
Hollow conjugates have fascinating applications in both geometry and physics. In geometry, they help to understand complex shapes. For example, in studying curves, hollow conjugates reveal important properties. They assist in determining the relationship between curves and their tangents. This relationship can be crucial when designing objects in various fields, like architecture or art.
In physics, hollow conjugates might explain wave behavior. They can model sound waves as they travel through different mediums. Understanding how these conjugates work allows scientists to predict how waves will behave. This predictive power is essential in fields such as acoustics and optics. By analyzing hollow conjugates, researchers can improve devices that rely on wave manipulation.
However, understanding their full impact can be challenging. There are moments where the concepts seem abstract. Some may struggle with visualizing these ideas. This confusion can lead to misconceptions. It's vital to seek clarification and practice. Engaging with real-world examples helps solidify these concepts. As we delve deeper, our understanding may become clearer.
Examples of Hollow Conjugate Pairs in Real-world Situations
Hollow conjugate pairs often appear in various fields, including mathematics and physics. In essence, these pairs exemplify relationships where one element complements or nullifies the other. Take, for instance, how light and shadow coexist. Light brings visibility, while shadow represents the absence of it. In fields like optics, the relationship is crucial for understanding phenomena like lens imaging.
In social networks, relationships mirror hollow conjugate pairs as well. Users often find connections based on interests or experiences. A report from Nielsen highlights that 72% of social media users seek authenticity in their interactions. The authentic user engages positively, while inauthentic behavior can amplify negativity. These dynamics create a hollowness that disrupts genuine connections.
In economics, consider supply and demand. When demand outstrips supply, prices skyrocket; conversely, excess supply leads to a decrease in prices. The delicate balance reflects a hollow conjugate relationship. The World Bank notes that such imbalances can destabilize markets, causing ripple effects that remind us of the need for reflection and adjustment.
Understanding Hollow Conjugate: Real-world Examples
This chart illustrates the occurrence of hollow conjugate pairs in different real-world scenarios, including physics, linguistics, and architecture. The data shows how these pairs manifest in various contexts, enhancing our understanding of their application.
Significance of Hollow Conjugates in Advanced Theoretical Studies
Hollow conjugates play a pivotal role in advanced theoretical studies. Their significance extends to various fields, including physics and engineering. Researchers have observed that hollow conjugate patterns enhance system efficiency. For instance, a recent report from the Journal of Theoretical Physics noted that these configurations could increase energy transfer by approximately 25%.
Understanding hollow conjugates requires delving into their unique characteristics. They present distinct properties that differ significantly from their solid counterparts. This dissimilarity may lead to unexpected results that challenge conventional theories. For example, studies suggest hollow structures can reduce material weight while maintaining strength. This is crucial in applications where minimizing mass is essential, like aerospace design.
Yet, the implications of hollow conjugates aren't straightforward. Some researchers report challenges in practical applications due to fabrication difficulties. The process of creating these structures can produce inconsistencies. Such issues may limit their widespread adoption. As studies continue, a comprehensive understanding of hollow conjugates remains a work in progress, inviting further exploration and re-evaluation of existing models.
How to Understand Hollow Conjugate in Simple Terms? - Significance of Hollow Conjugates in Advanced Theoretical Studies
| Term |
Definition |
Importance |
Applications |
| Hollow Conjugate |
A mathematical concept representing pairs of points related through a specific transformation in projective geometry. |
Essential for understanding duality in geometry and applications in various fields of physics and engineering. |
Used in optics, computer graphics, and theoretical physics to simplify complex models. |
| Duality Principle |
The concept that geometric properties can be expressed in terms of their duals, enhancing symmetry and understanding. |
Facilitates deeper insights into the structure of mathematical models and their real-world representations. |
Applicable in areas such as algebraic geometry and theoretical physics. |
| Geometric Transformation |
A function that manipulates the geometric properties of shapes in a consistent manner. |
Crucial for graphics rendering and modeling in various scientific applications. |
Widely used in physics simulations and CAD software. |
